【keras】オートエンコーダを用いた時系列データの異常検知を試す

深層学習を簡単に使用することができるkerasを使用して時系列データの異常検知について勉強していきたいと思います。

環境

こちらで構築したkerasの環境を使用します。

Windows10にKerasをインストールする – IT Learning (obenkyolab.com)

使用するデータ

kaggleに掲載されている以下のデータセットを使用させてもらいます。OpenDatabaseとして公開されていて非常にありがたいです。

Open Time Series Dataset | Kaggle

このデータセットの中には次の5つのカテゴリがあります。

Finance
Meteorology
Physics
Production
Sales

その中からPhysicsの中にある地震計の計測データを使うことにします。

Seismograph vertical acceleration nmsqsec of the Kobe earthquake recor.csv

データセットをkaggleのサイトからダウンロードしておきます。

異常検知の流れ

今回は地震計の測定データの中で「異常と思われる個所を赤く表示する」ということを試してみたいと思います。次のような流れで進めていきます。

データの中で正常と思われる個所と異常と思われる個所を取り出す
正常データで深層学習を行いモデルを作る
異常を含むデータをモデルに入力して検知させる
プロットする

また、今回オートエンコーダを勉強するにあたり、以下のkerasのチュートリアルのコードを参考にしました。

https://keras.io/examples/timeseries/timeseries_anomaly_detection/

正常・異常データの用意

まずは今回使用するデータをpandasで読み込んで確認して見てみます。

import pandas as pd
from matplotlib import pyplot as plt
df = pd.read_csv('Seismograph vertical acceleration nmsqsec of the Kobe earthquake recor.csv' ,parse_dates=True)
df.columns = ['times','x']
df.set_index('times', inplace = True)
fig, ax = plt.subplots()
df.plot(legend=False, ax=ax)
plt.show()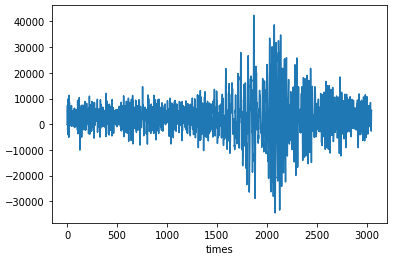

見た感じ、timesが1000くらいまでは振幅が落ち着いていて、1500-2500に大きくなっています。。

1500-2500の間に本当に現実として異常が発生したのかどうかはわかりませんが、今回は仮にtimesが0-1000の期間は正常で1500-2500は異常という風に考えることにします。

そのため、学習データとして0-1500の期間を取り出し学習データとし、1501-3000の区間を検証用の異常データ。

x = df[0:1500]
x_ano = df[1500:3000]

それぞれプロットして確認してみます。Y軸のスケールは-40000~45000の範囲で同じにしておきます。

正常

x.plot(legend=False)
plt.ylim([-40000, 45000])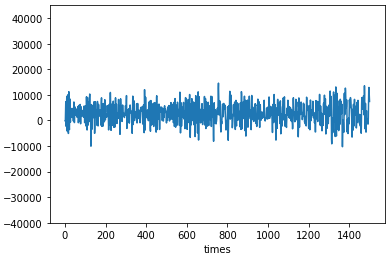

異常

x_ano.plot(legend=False)
plt.ylim([-40000, 45000])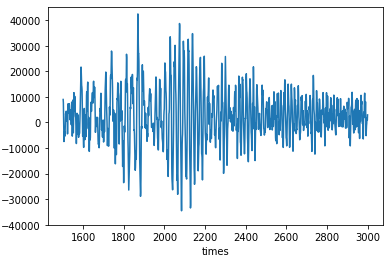

ここで、学習に使用する正常データを標準化しておきます。また、後ほど検証で使用する異常データについても併せて標準化しておきます。ここでポイントとしては、異常データの標準化の際に正常データの平均と標準偏差を使用することです。異常データについて、異常データの平均と標準偏差を使用してしまうと、正常時との比較で考えた場合に平等に評価できないという問題があるためです。

#標準化
x_norm = (x - x.mean())/x.std()
x_ano_norm = (x_ano - x.mean())/x.std()

学習用データの準備

次にデータを50点を1ずつスライドさせる関数を定義します。t_stepsがモデルに学習させる際の入力の次元になります。これは前述のkerasのチュートリアルを参考にしています。ステップ数などは適当に決めています。

import numpy as np
t_steps = 50
def create_sequences(df):
    x = []
    for i in range(0, len(df) - t_steps + 1):
        x.append(df[i:i + t_steps].to_numpy())
    x_out = np.array(x)
    return x_out

定義した関数を使用して、学習データに対してリストを生成します。

x_train = create_sequences(df_normalized)
x_train.shape

(1451, 50, 1)

モデルの定義

学習データのshapeに合わせた深層学習モデルのlayerをkerasのSequentialを使用して定義します。ポイントとしてはオートエンコーダとするため、畳み込みでサイズを変更したのち、最終的にConv1DTransposeで同じサイズに復元しています。また、最適化にはAdamを使用しています。

model =keras.initializers.Initializer()
model = keras.Sequential(
    [
        layers.Input(shape=(x_train.shape[1], x_train.shape[2])),
        layers.Conv1D(
            filters=32, kernel_size=7, padding="same", strides=1, activation="relu"
        ),
        layers.Dropout(rate=0.2),
        layers.Conv1D(
            filters=16, kernel_size=7, padding="same", strides=1, activation="relu"
        ),
        layers.Conv1DTranspose(
            filters=16, kernel_size=7, padding="same", strides=1, activation="relu"
        ),
        layers.Dropout(rate=0.2),
        layers.Conv1DTranspose(
            filters=32, kernel_size=7, padding="same", strides=1, activation="relu"
        ),
        layers.Conv1DTranspose(filters=1, kernel_size=7, padding="same"),
    ]
)
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.001), loss="mse")
model.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 conv1d (Conv1D)             (None, 50, 32)            256       
                                                                 
 dropout (Dropout)           (None, 50, 32)            0         
                                                                 
 conv1d_1 (Conv1D)           (None, 50, 16)            3600      
                                                                 
 conv1d_transpose (Conv1DTra  (None, 50, 16)           1808      
 nspose)                                                         
                                                                 
 dropout_1 (Dropout)         (None, 50, 16)            0         
                                                                 
 conv1d_transpose_1 (Conv1DT  (None, 50, 32)           3616      
 ranspose)                                                       
                                                                 
 conv1d_transpose_2 (Conv1DT  (None, 50, 1)            225       
 ranspose)                                                       
                                                                 
=================================================================
Total params: 9,505
Trainable params: 9,505
Non-trainable params: 0

いよいよ、作成したモデルに対して、学習用データをfitして学習していきます。

history = model.fit(
    x_train,
    x_train,
    epochs=200,
    batch_size=100,
    validation_split=0.1,
    callbacks=[
        keras.callbacks.EarlyStopping(monitor="val_loss", patience=5, mode="min")
    ],
)

...
Epoch 30/200
14/14 [==============================] - 0s 21ms/step - loss: 0.0273 - val_loss: 0.0182
Epoch 31/200
14/14 [==============================] - 0s 24ms/step - loss: 0.0266 - val_loss: 0.0183
Epoch 32/200
14/14 [==============================] - 0s 20ms/step - loss: 0.0259 - val_loss: 0.0203

学習曲線を確認してみます。

plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
plt.show()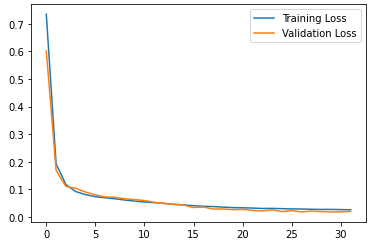

Validationデータに対する損失もトレーニングデータに対して下がっていっているので、良さそうです。

異常データの検出

ここから作成したモデルを使用して、異常データの検出を行っていきます。

まず、モデルに学習データを入力し、予測値を取得します。今回はオートエンコーダのため、入力に対して予測値も同じものが出てくるような想定です。この予測値に対して、実際の入力値との絶対誤差平均を計算し、絶対誤差平均の最大値を異常判定の閾値として使用することにします。

x_train_pred = model.predict(x_train)
train_mae_loss = np.mean(np.abs(x_train_pred - x_train), axis=1)
threshold = np.max(train_mae_loss)

次に、異常波形の入った検証用のデータをモデルの入力に合うよう学習データと同様にウィンドウを用いてデータセットを作成し、予測モデルに入力します。

得られた結果と入力の値における絶対誤差平均を計算し、絶対誤差平均が閾値異常になっているインデックスを抽出しておきます。

x_test = create_sequences(x_ano_norm)
x_test_pred = model.predict(x_test)
test_mae_loss = np.mean(np.abs(x_test_pred - x_test), axis=1)
test_mae_loss = test_mae_loss.reshape((-1))
anomalies = test_mae_loss > threshold

異常検出結果の確認

最後に、異常と判定されたインデックスを含んでいるデータセットに対して赤色でプロットします。

anomalous_data_indices = []
for data_idx in range(t_steps - 1, len(x_ano_norm) - t_steps + 1):
    if np.all(anomalies[data_idx - t_steps + 1 : data_idx]):
        anomalous_data_indices.append(data_idx)
        
df_subset = x_ano.iloc[anomalous_data_indices]
fig, ax = plt.subplots()
df.plot(legend=False, ax=ax)
df_subset.plot(legend=False, ax=ax, color="r")
plt.show()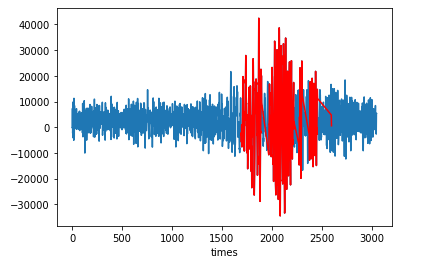

このように振幅が大きくなっている箇所が赤色で判定されました。

まとめ

今回はkerasのサイトにあるオートエンコーダのチュートリアルを参考にして、Kaggleのオープンデータを対象に異常検知を試してみました。パラメータについてはチュートリアルものをそのまま利用した部分もありましたが、それなりに検出できているような感じでした。今後もkerasのメソッドをいろいろと試してみたいと思います。