【Python】ヒストグラムの作成
目的
データ分析を行う際、まずはデータがどのように分布しているかをざっくりと確認し、それから分析の方針を決めたいという場面が多々あるかと思います。
そのため、今回はデータの分布状態を可視的に確認できるヒストグラムをpythonで表示する方法について学びたいと思います。
ヒストグラムとは?
繰り返しになりますが、データ全体の分布を分かりやすくまとめて可視化できるものがヒストグラムです。
ヒストグラムの具体的な作り方は以下の通りです。
- データをある範囲毎のグループにまとめる
- そのグループに所属するデータの数で集計する
- 横軸にグループ、縦軸にデータの数(度数)のグラフを描く
Sturgesの公式
さぁ、ヒストグラムを書こう、というときの最初の関門が 「データをある範囲毎のグループにまとめる 」という作業です。
具体的には、範囲毎のグループ(これを階級と呼びます)をどれだけの数用意すればよいかということで悩みます。グループをいくつ作るかです。
これはデータ全体の性質が大体分かっていれば何となく、何となく当たりをつけることができますが、データが膨大な場合などには頭を悩ませます。
そもそもデータ全体の性質をとらえるためにヒストグラムを書こうと思っているわけですので、このようなことは往々にしてあります。
しかし、素晴らしいことにこの当たりをつけてくれる公式があります。それがSturgesの公式というものです。
Sturgesの公式はデータ数から適当な階級の数はこれくらいがいいんじゃない、という答えを提案してくれます。
それでは実際の式を見ていきます。
いま、データ数を\(n\)とすると、 階級の数を\(k\)は以下の式で求めることができます。
$$k = 1+\log_2n$$
また、データの最小値と最大値の幅が\(R\)だとすると、この幅\(R\)を階級の数で割れば一つの階級における範囲が求まることになります。
つまり、階級の範囲\(c\)は以下で計算されます。
$$c=\frac{R}{1+\log_2n}$$
Pythonによるヒストグラムの描画
それでは実際のデータを使って、pythonでヒストグラムを書いてみたいと思います。
もちろん階級の数はSturgesの公式を用いて求めて使います。
まずは、データを準備します。
今回は、以下のサイトから福岡県のダムの貯水量のデータを使用させて頂きたいと思います。
https://www.open-governmentdata.org/
データの先頭5行は次のような形になっています。
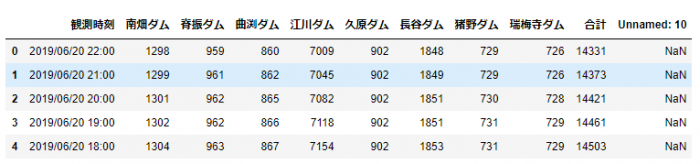
このデータにおける、南畑ダムの貯水量の値についてヒストグラムを描画してみます。
pythonのコードは以下になります。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt #描画用ライブラリ
#データ読み込み
df = pd.read_csv('C:\\201906data福岡市関連8ダム貯水量.csv',engine ='python')
#レコード数確認
n = len(df)
#Sturgesの公式より級数mを求める
m = 1 + np.log(n)/np.log(2)
print(m) #9.90388184573618
#級数mが整数でないため、四捨五入して整数型へ変換
m_int = int(round(m))
#pyplotにより求めた級数でヒストグラムを描画
plt.hist(df['南畑ダム'], bins = m_int)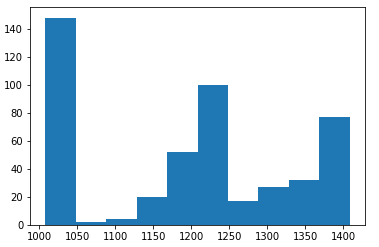
結果を見ると、なんとなく、1000~1050くらいのダム量が通常っぽいな、っということがなんとなーくわかりました。級数の数としてはまぁまぁな感じがします。
注意点
Sturgesの公式は万能ではありませんが、ヒストグラムを描画する際の最初の当たりをつけるのには使えると思います。実際は初期値をSturgesの公式でもとめ、その後自分でヒストグラムを描画してみながら、納得のいく級数の数にパラメータ調整していくのが良いかと思います。
