【Python】単回帰の計算と表示
目的
ある得られたデータをもとに、今後発生するデータが何かを予測したいという場合があります。例えば何かを販売しようと思ったときの需要予測であったり、株価の予測などです。このような予測問題を統計的に行う手法として回帰というものがあります。
今回はこの回帰という考え方について勉強したいと思います。
回帰の式
ある二つの変数\(Y\)と\(X\)があったときに、以下のような何らかの関数で互いの関係を表すことを回帰と呼びます
$$Y = f(X)$$
そしてこの\(f(X)\)が線形方程式の場合を線形回帰と呼び、非線形方程式の場合を非線形回帰と呼びます。
今回はよりシンプルな線形回帰を対象に考えます。そして、線形回帰の中でも最も分かりやすい単回帰という考え方について実践してみます。
単回帰とは?
シンプルに言うと、データ\(X\)とデータ\(Y\)の関係性を次のような一次の線形方程式で表すことです。
$$Y = aX+b$$
ただし、実際のデータは完全に上記の式にあてはまりません。一次の線形方程式は直線ですが、世の中で現実に発生するデータが全てきれいな直線上に乗ることはまずあり得ません。
そのため、単回帰とはデータ\(X\)と\(Y\)の関係性を線形の一次方程式で近似して表すという考え方になります。
ではどのように近似するかというと、最小二乗法という方法が用いられます。
最小二乗法
考え方はシンプルです。
まず、求めたいのは直線\(Y=aX+b\)の\(a\)と\(b\)です。
上記の直線において、データ\(X_i\)の時の\(Y\)の値は\(aX_i+b\)になります。
このとき、実際のデータ\(Y_i\)との偏差は\(Y_i- aX_i-b \)になります。
最小二乗の考え方はこの偏差の大きさが\(i=0~N\)にわたって最小になるものを探そうという考え方です。つまり、以下の式を最小にする\(a,b\)を求めるという方法です。
$$\sum_{i=1}^N(Y_i-aX_i-b)^2$$
二乗をとっているのは足し合わせる際に符号の正負で打ち消しあわないようにするためです。これは上記の式を\(a,b\)でそれぞれ偏微分することで求まります。
ただし、pythonでは式を直接書く必要はなく、メソッドを使うだけで簡単に算出できます。
pythonによる実装
pythonで単回帰を行うため、まず、データの準備をします。
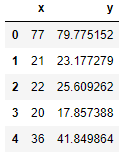
データはkaggleの線形回帰用のオープンデータを使用させてもらいます。データの先頭5行は以下のようになっています。
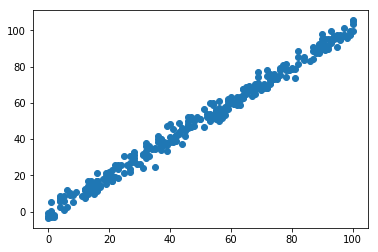
上記のデータについて、xを横軸、yを縦軸に散布図を描くと、下のようになります。さすが、線形回帰用のデータだけあって、見た目的にも一次の線形方程式にあてはまりそうです。
それでは、実際に\(y=ax+b\)となる\(a,b\)の組み合わせを求めます。
pythonのコードは以下になります。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#データ読み込み
df = pd.read_csv('C://test.csv',engine ='python')
# scikit-learnの linear_modelを読み込み
from sklearn import linear_model
#インスタンス作成
clf = linear_model.LinearRegression()
# x軸データ
x = df[['x']].values
# y軸データ
y = df['y'].values
# 単回帰モデルを作成
clf.fit(x,y)
# y=ax+bのaを表示
print(clf.coef_) #[1.01433536]
# y=ax+bのbを表示
print(clf.intercept_) #-0.4618107736611563
#散布図を表示
plt.scatter(x,y)
#回帰直線を表示
plt.plot(x, clf.predict(x),color = 'red')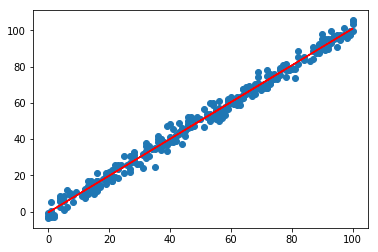
scikit-learn&matplotlibのライブラリを使うと、少ないコードで回帰計算と表示までできます。
注意点
単回帰は パラメータの数が\(a,b\)で求める式も シンプルですが、その分予測精度としてはそれほど良くない場合が多いです。そのような場合は重回帰や非線形回帰などでもフィットするか試してみる必要があります。
