Python statsmodelsで重回帰分析をする
概要
Pythonのライブラリであるstatsmodelsを使うことで重回帰分析を行う方法について説明します。データの分析ではなく、statsmodelsの使い方になれることを目的にします。
環境
- Python 3.8.6
- statsmodels 0.13.2
データ準備
今回はkaggleにOpenDatabaseとしてアップロードされているRed Wine Qualityのデータを例に使いたいと思います。まずはこのデータをKaggleのサイトからダウンロードします。
ライブラリインストール
重回帰分析に使用するstatsmodelsライブラリをインストールします。
pip install statsmodelsデータの読み込み
まずは、データを読み込んでいきます。
import pandas as pd
df = pd.read_csv('winequality-red.csv')
df.head()
qualityが応答変数で、そのほかの列を説明変数として扱えば良さそうです。
重回帰分析
早速重回帰分析を行います。statsmodelsは非常に便利で標準化などを行わないならほんの数行で重回帰分析の結果を出せてしまいます。
import statsmodels.api as sm
#quality列以外を説明変数として抽出
X = df[df.columns[:-1]]
#定数項の追加
X = sm.add_constant(X)
#応答変数の設定
y = df['quality']
#モデル生成(OLSは最小二乗法)
model = sm.OLS(y,X)
result = model.fit()
#結果表示
result.summary()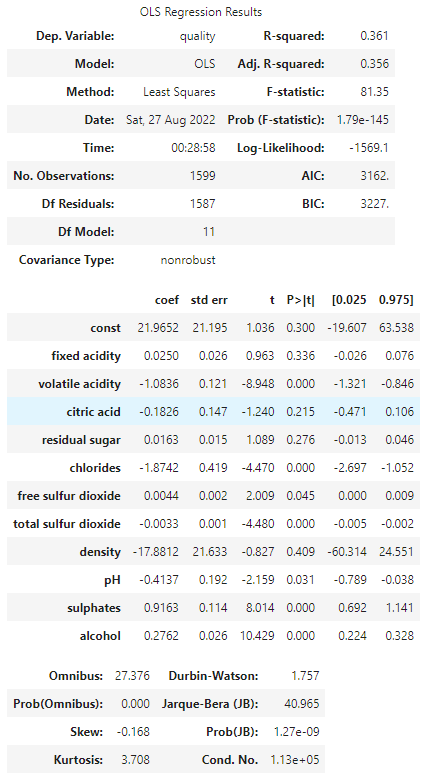
結果の見方
簡単に結果を出せたのは良いですが、結果の見方が分からないと意味がないため、調べていきます。
Dep. Variable
応答変数として指定した項目、つまりモデル作成時にyの値として指定したものが入ります。今回は応答変数としてqualityを指定しているため表示されています。
Model
どんなモデルを使用したかが表示されます。OLSはOrdinary Least Sqauaresのことで一般的にいう最小二乗法を使用したモデルのことです。model作成時にOLSを指定したためこれが表示されています。
Method
こちらもパラメータの決定手法が表示されています。Least Squaresは最小二乗法です。
Date, Time
サマリの表示を実行した日時が表示されます。
No. Observations
観測数、つまりデータの数です。今回は1599でlen(df)の結果と一致しました。
Df Residuals
分散分析表の残差における自由度が表示されます。残差の自由度は[データ数n] – [説明変数の数] – 1 となります。今回の場合、データ数が1599で説明変数の数が11ですので、1599 – 11 -1 = 1587 となっています。
Df Model
説明変数の数で11になります。
Covariance Type
説明変数間の共分散のタイプを表します。デフォルトでnonrobustとなっているようです。
R-squared
決定係数を表します。回帰の平方和を目的変数の総平方和で割ったものが決定係数です。
Adj. R-sqaured
自由度調整済み決定係数を表します。こちらは説明変数の数を加味して説明変数の数が異なるモデルの比較に使用できます。
F-statistic
F統計量です。計算された回帰モデルの説明変数の中に意味のある変数があるかどうかの検定に使用できるできる値です。
Prob (F-statistic)
F統計量の実現値(p値)です。今回は十分小さいことがわかります。
Log-Liklihood
対数尤度です。求めた回帰モデルから標本の尤もらしさを評価する値になります。
AIC
赤池情報量基準です。小さいほど良いとされます。
BIC
ベイズ情報量基準です。小さいほど良いとされます。
まとめ
statisticmodelsのライブラリはものすごく簡単に重回帰分析のサマリを出すことができてしまいます。ただ、実際の重回帰分析の際にはこのサマリだけでなく、他の指標などもグラフ化などして描画しながら多角的に見ていく必要があると思います。
