【Python】標準変化量と変異係数計算
概要
以前にデータの分散度を測る標準偏差という指標についてpythonで求めてみました。標準偏差はデータ全体の分散度を測ることができます。
次なる疑問として、ある標準偏差を持ったデータの集団の内、ある一つのデータに注目した時、そのデータがデータ全体のなかのどれくらいの位置に居るか、ということを評価できないか、ということが考えられます。
データの「まれ」さ
実は、データ全体の特性である 標準偏差が明らかになると、その中あるデータがそのデータ群の中でどれくらいの位置にいるかを測ることができます。
データの標準偏差を\(s\)とした場合、全データの約67%は\(x\pm s\)に入り、 約95%は\(x\pm 2s\) に入るということが言われています。
(ただしこれは データ\(x\)が正規分布に従っていると仮定した場合 )
つまり、分散度である標準偏差が小さいデータの集団においては、平均値から離れている値はより「まれ」な位置に存在しているということになり、逆に標準偏差が非常に大きいデータ群では少しくらい平均値から離れていても、それほどイレギュラーではない、と考えられるということです。
標準変化量
上記のように標準偏差の大きさと平均からの離れ具合を見てみることで、おおよそのそのデータの「まれ」さ具合は測れることがわかりました。
ただし、これはあくまでそのデータの集団の中においての話であり、ある集団の「まれ」さ具合を、他の集団に属するある値の「まれ」さ具合とそのまま比較することはできません。
どういうことか例を挙げて考えてみます。
例えば、県内の20代の人の100m走の平均が14秒、標準偏差が2秒だったとします。
自分も走ってみたところ、結果が12.3秒だったとします。まぁまぁ良い結果な感じがします。
次に、同じく県内の20代の人の10キロマラソンの平均が60分で標準偏差10分だとします。
自分も走ってみたら、結果が59分だったとします。こちらも平均以上で良い感じがします。
このような場合に、自分は短距離と長距離のどちらが得意科目といえるか?と考えたくなります。
もちろん、標準偏差だけで比較することはできません。
そこで登場するのが標準変化量という考え方です。
いま、標準変化量を\(z\)とすると、以下の式で定義されます。
$$z = \frac{x-\overline{x}}{s}$$
上記はあるデータ平均からの偏差が標準偏差の何倍であるかを表している式になっており、データの集団間で比較可能な相対的な度合いとなっています。
先ほどの短距離と長距離の結果を例にして、実際に計算してみます。
短距離:
$$z = \frac{12.3-14}{2} = -0.8$$
長距離:
$$z = \frac{59-60}{10} = -0.1$$
絶対値で比較すると、短距離のほうが値が大きく、より「まれ」な値と評価できます。つまり、短距離のほうが得意と言えるということです。
Pythonによる標準変化量の計算
この標準変化量をpythonで計算してみたいと思います。
まずはデータ準備です。
データセットとして、kaggleから以下のオープンデータをダウンロードして使用させてもらいます。
Los Angeles General Fund Revenue
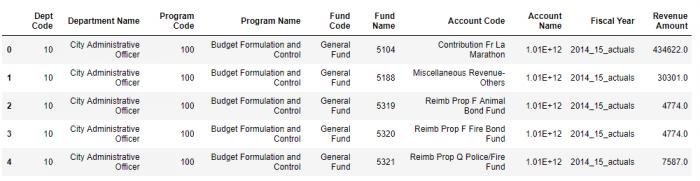
このデータセットのRevenue Amountの列データに対して標準変化量を求めてみようと思います。
以下のようなコードで計算できます。標準変化量は各データについて計算されます。
import pandas as pd
#データの読み込み
df = pd.read_csv('C:\\general-fund-revenue.csv',engine ='python')
#各データにおける標準変化量を計算
(df['Revenue Amount']-df['Revenue Amount'].mean())/df['Revenue Amount'].std()
----
0 -0.102793
1 -0.110366
2 -0.110844
3 -0.110844
4 -0.110792
5 -0.109117
6 -0.102917
7 -0.106688
8 -0.110723
9 -0.110000
10 -0.110300
11 -0.110611
12 -0.102445
13 -0.102649
14 -0.104650
...
4858 -0.073472
4859 -0.104867
4860 -0.093327
4861 0.737893
4862 0.810207
4863 -0.104367
4864 -0.062064
4865 -0.110915
4866 -0.084710
4867 4.347067
4868 -0.002459
4869 0.490626
Name: Revenue Amount, Length: 4870, dtype: float64変異係数
データの「まれ」さ具合を異なる集団で相対比較するには標準変化量が使えることが分かりましたが、データのばらつき自体をデータの集団間で比較したいような場合もあります。
その比較ができる指標が変異係数\(CV\)というものです。
以下の式で定義されます。
$$CV=\frac{s}{\overline{x}}$$
式としては非常にシンプルで、標準偏差をデータの平均値で割った値になっています。
つまり、データの平均の値が大きければ、たとえ標準偏差が大きくてもCVはそれほど大きくなりません。
逆に標準偏差が小さくても、データの平均値が大きければCVは大きくなります。
よって、データの集団をまたいで、相対的にばらつき具合を比較できる指標になっています。
では、この変異係数についてもRevenue Amountのデータを使って計算してみたいと思います。
pythonのコードは以下になります。
df['Revenue Amount'].std()/df['Revenue Amount'].mean()
#結果:9.01437624937767pythonを使用するとこのような指標も簡単に計算できました。
