【Python】算術平均と幾何平均計算
目的
統計学を使いこなしたい。
でも参考書を読んでいても難しい概念や数式が沢山出てきて、その時は分かったつもりになっても後で実践的に使う場面でなかなか使えてない。
やはり自分は参考書を読むだけでなく、実際のデータをpythonで扱い、手を動かしながら(コードを書きながら)統計学の勉強をしていきたい。
そのため、統計学の基本部分からpythonでコーディングしていきます。
平均
まずは、これから。小学生でも習うであろう平均という統計値に対して、データを触りながら理解を深めていきたいと思います。基本が大事です。
算術平均
世の中一般で言う「平均」が算術平均です。
例えば3人の人が居て、それぞれ、次ような身長だったとします。
- Aさん 170cm
- Bさん 165cm
- Cさん 175cm
このとき、当たり前ですが、3人の身長の平均(算術平均)は以下のように計算できます。
(170+165+175)÷3 = 170cm
これが算術平均の計算方法ですが、平均には上記とは異なる定義と計算方法があります。
幾何平均
その他の平均の定義として幾何平均というものがあります。
幾何平均で計算したいケースは、比率の平均をとりたいような場合です。例えばGDPの成長率を計算したいような時です。
具体的なイメージがわかりやすいように実際のGDPのデータを用いて計算してみたいと思います。
データは内閣府HPにオープンデータとして公開されており、こちらからダウンロードできます。
上記から取得したデータを使って以下のようなデータを作りました。
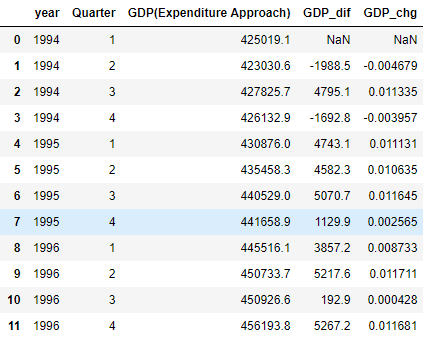
GDP(Eexpenditure Approach)を各年の各クウォータのGDPとします。
また、GDP_difを前クォータとの差分、GDP_chgを前クォータとの差分の比率とします。
ここから幾何学平均を計算していきます。
まず、GDPの平均伸び率を計算したい場合、もし単純に先述の算術平均を使って計算すると、pythonの.mean()を使用することで、以下のようなコードで計算できるかと思います。
#GDP成長率計算
GDP_df['GDP_chg'].mean()+1 #結果:1.006475286192290905
では次に、このような場合に算術平均が適当か?ということを考えるために、まずは、GDPの伸び率がどのような計算で行われているかを再確認してみます。
1994年の第一期のGDPを初期値\(A_0\)としたとき、\(N\)期後のGDP(\(A_N\)とする)を比率\(r_i\)を使って計算すると次のようになります。
$$A_N=A(1+r_0) (1+r_1)… (1+r_N) $$
ここで、仮に伸び率の平均値の\(\overline{r}\)というものが存在したとすると、以下のような計算式になるのが自然に思えます。
$$A_N=A(1+\overline{r}) (1+ \overline{r} )… (1+ \overline{r} ) =A(1+\overline{r})^N $$
これを変形すると以下になります。
$$\overline{r} = \sqrt[ n ]{ (1+r_0) (1+r_1)… (1+r_N) } -1$$
$$ 1+\overline{r} = \left(\prod_{i=0}^{n} (1+r_i)\right) ^\frac{1}{n} $$
上記を見ると、成長率の平均は各クォータの成長率の積\(n\)乗根になっていることが分かります。
これを幾何平均と呼びます。
このように、○○率のような比率に対して平均をとる場合には算術平均でなく幾何平均の方が自然な場合があります。
幾何平均をpythonで計算するには以下のコードでできます。
from scipy import stats
#1を足して1+rの形にする
GDP_df['GDP_chg_1r'] = GDP_df['GDP_chg']+1
#1行目の成長率はnanなため、2行目から幾何平均をとる
stats.gmean(GDP_df['GDP_chg_1r'][2:]) #結果:1.0075758730457869算術平均の場合はGDP伸び率の平均が1.006475だったのに比べ、幾何平均の場合は1.007576と少し大きくなりました。
まとめ
平均には一般的に使う算術平均のほか、幾何学平均というものも存在する。
データ群に対して、モデル化などを行う際、代表値の選び方で幾何平均を選択したほうが、よりフィットする場合もあろうかと思います。
