【Python】四分位数の計算
目的
これまで、データの平均の考え方とその計算方法について学びました。
しかし、データの特性の評価には平均だけでなく、ばらつきも重要です。
今回はデータのばらつきの考え方である四分位数とpythonによるその計算方法について勉強したいと思います。
データ準備
四分位数をpythonで触りながら理解するために、ある程度の行数を持ったデータを使いたいと思います。
今回はkaggleというサイトでオープンデータとして公開されている、アボカドのpriceデータをダウンロードして使ってみたいと思います。
なお、元は以下のサイトから提供されています。
https://hassavocadoboard.com/
まずはpythonのpandasライブラリのread_csvで読み込みます。pandasのread_csvメソッドでcsvファイルを読み込むと、読み込んだデータがDataFrame型で格納されるため、その後の扱いが便利になり、おすすめです。
実際の読み込みのコードは以下になります。pythonの読み込みではパスの書き方で\を重ねる必要があるので注意してください。
import pandas as pd
#ファイルをDataFrame型で読み込み
df = pd.read_csv('C:\\avocado.csv',engine ='python')
#先頭5行を表示
df.head()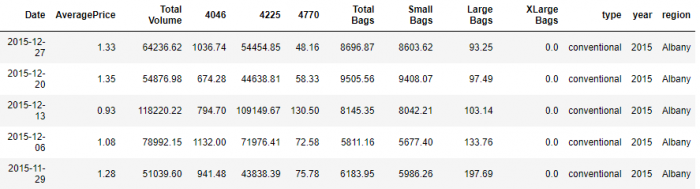
データの中身としてはDateカラムに日付、AveragePriceカラムに価格データなどが格納されています。今回はAeragePriceのカラムのデータを使用します。
四分位数
データのばらつき(分散度)を測るための指標として四分位数をという考え方を使う方法があります。
まずは四分位数とは何かから理解します。
四分位数の定義
データを小さいほうから順に並べた場合に、これらを4等分する3つのデータのことを指します。この3つのデータをそれぞれ第1四分位数Q1、第2四分位数Q2、第3四分位数Q3といいます。
先ほどのAveragePriceのデータを例にして考えると、価格の安い順から順番に並べた場合それらを4等分する位置にいるデータが四分位数になります。
ではこの四分位数をpythonで計算してみたいと思います。
読み込んだデータのAveragePriceのカラムのデータを使います。
pandas quantileメソッドの引数には下から順番に並べた際の割合部分を入れます。四分位数の場合は0.25,0.5,0.75を使います。
#第一四分位数を計算
Q1 = df['AveragePrice'].quantile(.25)
#第二四分位数を計算
Q2 = df['AveragePrice'].quantile(.50)
#第三四分位数を計算
Q3 = df['AveragePrice'].quantile(.75)
#結果の表示
print("Q1:",Q1) # Q1: 1.1
print("Q2:",Q2) # Q2: 1.37
print("Q3:",Q3) # Q3: 1.66四分位偏差
前述までで四分位数Q1,Q2,Q3が求まりました。
ここからが本題である四分位数を使ってばらつきを測る方法です。データのばらつき(分散度)は四分位偏差として定義されている以下の計算式で測ります。
$$\frac{Q_3-Q1}{2}$$
四分位数が求まっていれば、非常に簡単に計算できます。
pythonのコードも次のようなシンプルな演算の記述だけで求まります。
(Q3-Q2)/2 #0.1449999999999999この計算の意味はデータを小さい順に並べた際時に、ちょうど25%の位置にくるデータと75%の位置にくるデータとの差を2で割った値になります。
何故2で割るかというと第二四分位数からの偏差としてみることができるからです。
注意点
上記のように四分位偏差という代表値を用いて簡単にデータのばらつき具合を測ることができます。
ただし、四分位偏差の計算はデータすべてを計算に使っているわけではないため、データの特性を十分に表現できているかというと微妙なところもあるため注意が必要です。

