【Pythonテクニカル分析】エルダー・レイの計算と描画
エルダー・レイはモメンタム系のテクニカル分析手法になります。エルダー・レイはブル・パワーとベア・パワーの計算が必要であり、これらの計算にはEMA(指数平滑化平均)を求める必要があります。全体的に計算自体はシンプルなコードで記述できます。
EMAの計算についてはこちらを参考にしてください。
【Python】pandas DataFrameによる指数荷重計算(EMA) – Obenkyolab
ブル・パワー/ベアパワーの計算
ブルパワーとベアパワーはそれぞれ以下のように計算されます。
ブル・パワー = 当日の高値 – EMA
ベア・パワー = 当日の安値 – EMA
以下が日経平均で実際にブル・パワーとベア・パワーを計算する例になります。EMAは13日の平滑平均を用います。
# ライブラリの読み込み
import pandas_datareader as pdr
from datetime import datetime, timedelta
import pandas as pd
# データ取得期間設定
current_date = datetime.now()
two_years_ago = current_date - timedelta(days=365) # 1年前を設定
formatted_date = two_years_ago.strftime("%Y-%m-%d")
df = pdr.DataReader('^NKX', 'stooq',start=formatted_date) # データの取得
df.sort_values('Date', inplace=True) # 日付順にソート
# EMA計算用関数
def ema(df,span):
EMA = df['Close'].ewm(span=span, adjust=False).mean()
return EMA
# ブル・パワー
bullspower = df['High'] - ema(df,13)
# ベア・パワー
bearspower = df['Low'] - ema(df,13)描画
ブル・パワーとベア・パワーは平滑平均とスケールが異なるため、右側に第二軸を用意して描画すると見やすくなります。
import matplotlib.pyplot as plt
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.plot(ema(df, 13), label='EMA')
ax1.legend()
ax2 = ax1.twinx()
ax2.plot(bullspower, color='green', label='signal')
ax2.plot(bearspower, color='orange', label='signal')
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1+h2, l1+l2, loc='upper left')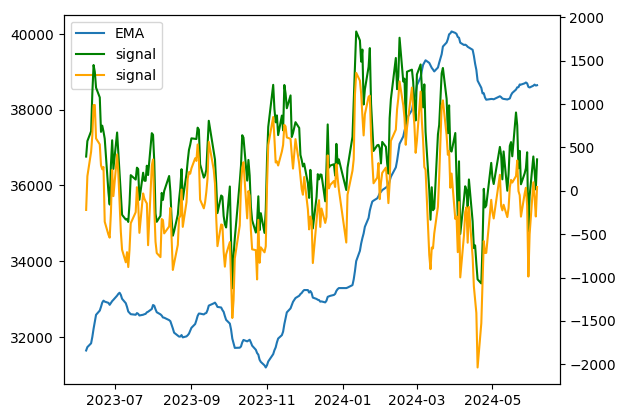
このようにしてエルダー・レイを計算し、描画することができました。
